حل كتاب الرياضيات للصف الثامن الوحدة الثامنة الاشكال الرباعية
نقدم لكم حل كتاب الرياضيات للصف الثامن الوحدة الثامنة الاشكال الرباعية يتضمن الملف حل الأنشطة والتقويم ( الوحدة الثامنة الاشكال الرباعية) في مادة الاشكال الرباعية للصف الثامن
حل كتاب الرياضيات للصف الثامن الوحدة الثامنة الاشكال الرباعية بإمكانكم تحميل هذا الملف على شكل بي دي إف PDF جاهز للتشغيل على أي جهاز لوحي أو إلكتروني أو كمبيوتر عن طريق زر التحميل في الأعلى كما يمكنكم تصفح الملف فقط من خلال هذه الصفحة من الموقع مباشرة
تصاميم هندسية
مشروع الوحدة : تصاميم هندسية
عمليات التصميم الهندسي هي مجموعة من الخطوات التي تتم من اجل اخراج منتج جديد او نظام جديد
خطة العمل :
1 - توظيف اشكال رباعبة لتكوين تصاميم هندسية متنافسة و مميزة
خطوات تنفيذ المشروع :
1 _ في تصميمك ارسم شكلا رباعية مستخدما شبكة المربعات ادوات هندسية
2 _ ضمن في تصميمك كل انواع متوازيات الاضلاع مستطيل و معين و مربع
3 _ حدد الاشكال الرباعية المستخدمة في التصميم و حلل خواصها من حيث التطابق و التماثل و الخ …
4 _ استخدم اكثر عدد ممكن من الاشكال الرباعية لتكون التصميم
علاقات التواصل :
1 _ المجموعة الواحدة تصميم عدة تصاميم هندسية و يتم اختيار الافضل
عرض العمل :
1 _ كل مجموعة تعرض التصميم النهائي مع الجدول المستخدم
المستقيمات المتوازية
سوف نتعلم العلاقة بين الزوايا الناتجة من قطع مستقيم لمستقيمين متوازيين
تسمى الخطوط المستقيمة التي تقع في مستوى واحد و لا تتقاطع ابدا بالخطوط المتوازية

نشاط 1 :
أ _ اكمل ما يلي : عندما يقطع مستقيم مستقيمين تنتج زوايا عدددها ..8… من هذه الزوايا زوايا متبادلة و زوايا …متناظرة… و… متحالفة… و… متقابلة بالرأس… و … متجاورة…
ب _ اكمل الجدول التالي :
| ازواج من الزوايا المتبادلة | داخليا : 4 , 6 _ 3 , 5 خارجيا : 2 , 8 _ 7 , 1 |
| ازواج من زوايا المتناظرة | 1 , 5 _ 4 , 8 - 3 , 7 - 2 , 6 |
| ازواج من الزوايا المتحالفة | 4 , 5 - 3 , 6 |
| ازواج من الزوايا المتقابلة بالرأس | 1 , 3 - 2 , 4 - 5 , 7 - 6 , 8 |
| ازواج من الزوايا المتجاورة | 1 , 2 - 1 , 4 - 4 , 3 - 2 , 3 - 5 , 6 - 5 , 8 - 8 , 7 - 6 , 7 |
تذكر ان :
1 _ الزاويتان المتكاملتان مجموع قياسهما 180
2 _ الزاويتان المتتامتان مجموع قياسهما 90
ربط الافكار :
اذا قطع مستقيم مستقيمين متوازيين فان :
1 _ كل زاويتين متبادلتين متطابقتين
2 _ كل زاويتين متناظرتين متطابقتين
3 _ كل زاويتين متخالفتين متكاملتان
تدرب 1 :
في كل من الاشكال التالية اوجد قيمة س مع ذكر السبب ؟

125 65 70 60
بالتناظر و التوازي بالتبادل و التوازي بالتحالف و التوازي متبادلتان خارجا مع التوازي
تذكر ان :
1 _ الزاويتان المتجاورتان على خط مستقيم واحد متكاملتان
2 _ الزاويتان المتقابلتان بالراس متطابقتان
تدرب 2 :
في الشكل المقابل : ا ب \\ ج د , و ه قاطع لهما في ن , م على الترتيب و ن ب = 115 فاكمل لنوجد بالبرهان ج م ن
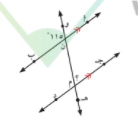
المعطيات : 1 _ أ ب \\ ج د , و ه قاطع لها
2 _ و ن ب = 115
المطلوب : ايجاد ج م ن
البرهان : أ ب \\ ج د , و ه قاطع لها ( معطى )
و ن ب = 115 ( معطى )
ق ( ن م د ) = ق ( و ن ب ) = 115 ( بالتوازي و التناظر )
ق ( ج م ن ) = 180 - 115 = 65 لان ح م ن , ن م د متجاورتان على مستقيم
فكر و ناقش : قال عبد الكريم استطيع حل تدريب 2 السابق بطرق اخرى مختلفة فهل توافقه الرأي ؟ فسر اجابتك ؟
نعم , مثلا ب ن م = 65 بالتجاور على المستقيم مع و ن ب , ب ن م = ج م ن بالتبادل و التوازي
نتيجة :
1 _ زاويتان متبادلتان متطابقتان
2 _ زاويتان متناظرتان متطابقتان
3 _ زاويتان متحالفتان متكاملتان
فإن المستقيمين يكونان متوازيين
اذا قطع مستقيم مستقيمين في المستوى و كان :
1 _ الزاويتان المتبادلتان 1 , 2 فإن ل 1 \\ ل 2
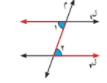
2 _ الزاويتان المتناظرتان 1, 2 متطابقتان فان ل 1 \\ ل 2
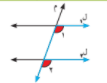
3 _ الزاويتان المتحالفتان 1, 2 متكاملتان فان ل 1 \\ ل 2
تمرن :
في الشكل المقابل س ص \\ ع ل
ق ( ع ب م ) = 40 , ق ( ا ج ب ) = 65 اوجد بالبرهان كلا من : ق ( ص ا ج ) , ق ( س ا ب ) , ق ( ج ا ب )
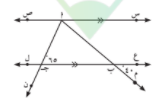
الحل :
1 _ق ( ص ا ج ) = ق ( ا ج ب ) = 65 بالتبادل و التوازي
2 _ ق ( ا ب ج ) = ق ( ع ب م ) = 40 زاويتان متقابلتان بالرأس
3 _ ق ( س ا ب ) = ق (ا ب ج ) = 40 بالتبادل و التوازي
4 _ ق ( ج ا ب ) = 180 - ( 65 + 40 ) = 75 مجموع قياسات زوايا المثلث 180
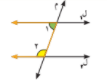
2 _ في الشكل ا , ب ضع قياسا من عندك لاحدى الزاويتان 1 , 2 او كلتيهما لنجعل ل , م متوازيين
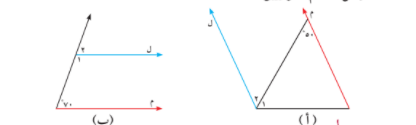
ق 2 = 50 ق 1 = 110 بالتحالف و التوازي
ق 1 = اجابات متعددة ق 2 = 70 بالتناظر و التوازي
في الشكل المقابل و حسب البيانات المحددة عليه اثبت ان م ن \\ ص ع
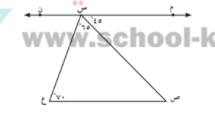
ق ( س ص ع ) = 180 - ( 65 + 70 ) = 45 مجموع قياسات زوايا المثلث 180
ق ( س ص ع ) = ق ( م ش ص ) = 45 بالتبادل و التوازي اذا م ن \\ ص ع
في الشكل المقابل و حسب البيانات المدونة عليه برهن ان س ل \\ ص ع , س ص \\ ل ع
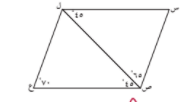
ق ( س ل ع ) = ق ( ل ص ع ) = 45 هما في وضع تبادل و توازي اذا س ل \\ ص ع
ل ص ع فيه : ق ( ص ل ع ) = 180 - 110 = 65 مجموع قياسات زوايا المثلث 180
ق ( س ص ل ) = ق ( ع ل ص ) = 65 هما في وضع التبادل س ص \\ ل ع
في الشكل المقابل و حسب البيانات المحددة عليه اثبت ان ج ه \\ ب ا
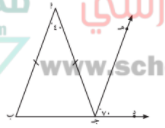
( ا ب ج ) متطابق الضلعين
ق ( ا ب ج ) = ق ( ا ج ب ) = 180 - 40 ÷ 2 = 70
ق ( ا ب ج ) = ق ( ه ج د ) = 70 هما في وضع تناظر و توازي ج ه \\ ب ا
في الشكل المقابل و حسب البيانات المحددة عليه اثبت ان
1 _ س م ص = ع م ل
2 _ س ص \\ ع ل
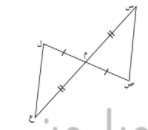
س م ص , ع م ل فيهما
س م = ع م معطى
ص م = ل م معطى
ق ( س م ص ) = ق ( ع م ل ) بالتقابل بالراس
س م ص = ع م ل بحالة ( ض ز ض )
من تقابل المثلثين نستنتج ق ( س ) = ق ( ع ) و هما في وضع تبادل س ص \\ ع ل

