عزيزي طالب الصف الثامن هل تبحث عن كتاب الرياضيات للصف الثامن الفصل الثاني ؟ في هذا الملف سوف نعرض لكم كتاب الرياضيات للصف الثامن الفصل الثاني
وحدة الأشكال الرباعية
درس المستقيمات المتوازية
نشاط 1 :
أ _ اكمل ما يلي : عندما يقطع مستقيم مستقيمين تنتج زوايا عدددها ..… من هذه الزوايا زوايا متبادلة و زوايا …… و… … و… … و ……
ب _ اكمل الجدول التالي :
| ازواج من الزوايا المتبادلة | داخليا : خارجيا : |
| ازواج من زوايا المتناظرة | |
| ازواج من الزوايا المتحالفة | |
| ازواج من الزوايا المتقابلة بالرأس | |
| ازواج من الزوايا المتجاورة |
تذكر ان :
1 _ الزاويتان المتكاملتان مجموع قياسهما 180
2 _ الزاويتان المتتامتان مجموع قياسهما 90
ربط الافكار :
اذا قطع مستقيم مستقيمين متوازيين فان :
1 _ كل زاويتين متبادلتين متطابقتين
2 _ كل زاويتين متناظرتين متطابقتين
3 _ كل زاويتين متخالفتين متكاملتان
تدرب 1 :
في كل من الاشكال التالية اوجد قيمة س مع ذكر السبب ؟

تذكر ان :
1 _ الزاويتان المتجاورتان على خط مستقيم واحد متكاملتان
2 _ الزاويتان المتقابلتان بالراس متطابقتان
تدرب 2 :
في الشكل المقابل : ا ب \\ ج د , و ه قاطع لهما في ن , م على الترتيب و ن ب = 115 فاكمل لنوجد بالبرهان ج م ن
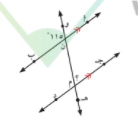
المعطيات : 1 _
2 _
المطلوب : ايجاد ج م ن
البرهان : أ ب \\ ……… قاطع لها ( معطى )
و ن ب = ….. ( معطى )
ق ( ن م د ) = ق ( و ن ب ) = …….. ( بالتوازي و التناظر )
ق ( ج م ن ) = 180 - 115 = 65 لان
فكر و ناقش : قال عبد الكريم استطيع حل تدريب 2 السابق بطرق اخرى مختلفة فهل توافقه الرأي ؟ فسر اجابتك ؟
نتيجة :
1 _ زاويتان متبادلتان متطابقتان
2 _ زاويتان متناظرتان متطابقتان
3 _ زاويتان متحالفتان متكاملتان
فإن المستقيمين يكونان متوازيين
اذا قطع مستقيم مستقيمين في المستوى و كان :
1 _ الزاويتان المتبادلتان 1 , 2 فإن ل 1 \\ ل 2
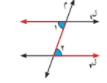
2 _ الزاويتان المتناظرتان 1, 2 متطابقتان فان ل 1 \\ ل 2
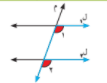
3 _ الزاويتان المتحالفتان 1, 2 متكاملتان فان ل 1 \\ ل 2
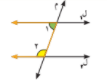
تمرن :
في الشكل المقابل س ص \\ ع ل
ق ( ع ب م ) = 40 , ق ( ا ج ب ) = 65 اوجد بالبرهان كلا من : ق ( ص ا ج ) , ق ( س ا ب ) , ق ( ج ا ب )
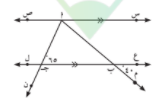
2 _ في الشكل ا , ب ضع قياسا من عندك لاحدى الزاويتان 1 , 2 او كلتيهما لنجعل ل , م متوازيين
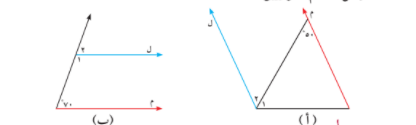
في الشكل المقابل و حسب البيانات المحددة عليه اثبت ان م ن \\ ص ع
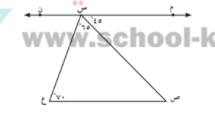
في الشكل المقابل و حسب البيانات المدونة عليه برهن ان س ل \\ ص ع , س ص \\ ل ع
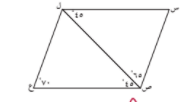
في الشكل المقابل و حسب البيانات المحددة عليه اثبت ان ج ه \\ ب ا
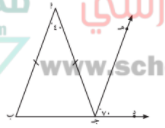
في الشكل المقابل و حسب البيانات المحددة عليه اثبت ان
1 _ س م ص = ع م ل
2 _ س ص \\ ع ل
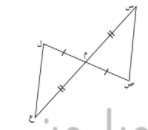
درس متوازي الأضلاع و خواصه
تدرب في الشكل المقابل متوازي اضلاع اوجد محيط متوازي المتوازي الأضلاع لإيجاد المحيط نوجد باقي أطوال أضلاع
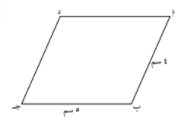
متوازي الأضلاع :
د جـ = ….. السبب :
أد = …… السبب :
محيط متوازي الأضلاع =
تدرب 2 :
أ ب جـ د متوازي أضلاع ق ( أ ) = 65 اوجد ق ( ب ) ق ( د )
المعطيات : ( ١ ) أ ب ج ـد متوازي أضلاع ، ( ٢ ) ; ق ( أ) = 65
المطلوب : إيجاد قياس ….
البرهان : ∵ أ ب جـ د متوازي أضلاع
ب = 180 - …. = …. ( لان كل زاويتين متتاليتين ………)
ج = ……….. = …… ( لان كل زاويتين ……. )
د = ……… = …….. ( لان كل زاويتين متقابلتين …… )
تدرب 3 :
ل م ن ع متوازي أضلاع تقاطع قطريه في و .
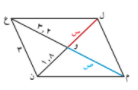
أوجد : ( ١ ) س ،ص . ( ٢ ) محيط المثلث ل م و
∵ الشكل ل م ن ع (………. )
∴ القطران ……….
∴ س = = ١٫٨ وحدة طول ،
و بالمثل ص = …………………. = ٣٫٢ وحدة طول
∴ محيط Δ ل م و = …………
تدرب 4 :
في متوازي الأضلاع المقابل ،
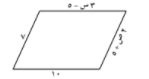
أوجد قيمة كل من س ، ص .
∵ من خواص متوازي الأضلاع كل ضلعين متقابلين متطابقان :
١٠ = ٥ - س ٣ : فيكون
……. + ١٠ = س ٣
٣ س = …..
س = ……..
٧ = ٥ + ص ٢ : بالمثل
ص = …
مما سبق : تحققنا من صحة خواص متوازي الأضلاع و هي :
١ _ في متوازي الأضلاع كل ضلعين متقابلين متطابقان
٢ _ في متوازي الأضلاع كل زاويتين متقابلتين متطابقتان
٣ _ في متوازي الأضلاع القطران ينصف ّكل منهما الآخر
تدرب :
إذا كان أ ب جـ د متوازي أضلاع و كان الفرق بين أي زاويتين غير متقابلتين ٤٠، ° فما هو قياس الزاوية الصغرى لمتوازي الأضلاع ؟
درس المستطيل و خواصه
تدرب :
استخدم المعطيات ( موظفا التعريف ) التي على الأشكال لتبين اياً منها تمثل مستطيلا ؟
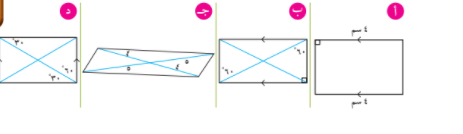
مما سبق نقول َّإن متوازي الأضلاع يكون مستطيلا إذا توفرت فيه أحد الشروط التالية :
١ _ إحدى زواياه قائمة .
٢ _ قطراه متطابقان
تدرب :
ك ص ع ل متوازي أضلاع فيه : ك ع = ٧ وحدة طول ، ص م = ٣٫٥ وحدة طول .
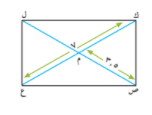
أثبت َّأن : ك ص ع ل مستطيل
المعطيات : ( ١ ) ك ص ع ل متوازي أضلاع
( ٢ ) ك ع = ٧ وحدة طول ، ص م = ٣٫٥ وحدة طول
المطلوب : اثبات ان ك ص ع ل مستطيل
البرهان : ∵ ك صع ل ( معطى )
∴ص م = …..= ………، القطران
ص ل = ……….
∴ ك ع = …………= ٧ ، القطران
∴ الشكل ك ص ع ل………………. َّلأن ك ص ع ل شكل متوازي أضلاع فيه ……..
درس المربع و خواصه
تدرب :
أ ب جـ د ، هـ ب جـ و متوازيا أضلاع .
د ، هـ ينتمي أ و بحيث د هـ = ب جـ ، أ ب = و جـ
أثبت َّأن : د ب جـ هـ مستطيل .
المعطيات :
المطلوب : أثبت ان ……..
البرهان :
∵ أ ب ج ـد ، هـ ب جـ و ( معطى )
∴ $د // ب جـ ، هـ و // ( من خواص )
∵ د ، هـ x ( معطى )
∴ د هـ // ……… 1
د هـ = ( معطى ) 2
من ( ١ ) ، ( ٢ ) ينتج َّأن :
د ب جـ هـ ………..( َلأنه شكل رباعي فيه ضلعان متقابلان ) 3
∵ $ ب = …………ز، و جـ = ……………….( من خواص متوازي الأضلاع )
∵ $ ب = و جـ ( معطى )
∴ $ ب = د جـ = ب هـ = و جـ ( من خواص المساواة )
∴ د جـ = ، ∴ القطران متطابقان 4:
من ( ٣ ) ، ( ٤) ينتج َّأن :
الشكل د ب جـ هـ مستطيل ( َّلأنه متوازي أضلاع فيه )
وحدة المقادير الجبرية
درس قوانين الأس
اكمل الجدول التالي :
| الصورة الاسية | الاساس | الاس | صورة الضرب المتكرر | الناتج |
| 4 ^2 | 4 | 2 | 4 × 4 | 16 |
| 3 ^5 | 3 | 5 | 3 × … × … × … × … | 243 |
| 2 ^4 | 2 | 4 | 2 × 2 × 2 × 2 | 16 |
| 5- ^3 | 5 - | 3 | 5 - × - 5 × - 5 | 125 - |
| 3 | 3 | 1 | 3 | 3 |
| س ^4 | س | 4 | س × س × س × س | س^3 |
| 3 5 - ^2 | 3 5 - | 2 | 9 25 | |
| 1 2 ^4 | 1 2 | 4 | 1 2 × 1 2 × 1 2 × 1 2 | 1 16 |
نشاط 2 :
اكمل ما يلي :
2 ^2 × 2 ^3 = 2 × 2 × 2 × 2 × 2 × 2 = 2^(2 + 3 )
3 ^ 2 × 3 ^ 4 = 3 × 3 × 3 × … × … × … = 3 ^… = 3 ^(2 + 4)
ماذا تلاحظ ؟
تدرب 2 :
اختصر كلا مما يلي :
1 _ 6 ^ 4 × 6 ^ 7 = 6 ^( … + 7) = 6 ^…
2 _ س^2 × س^3 = س ^ (2 + 3) =س ^5
3 _ ص × ص ^2 × ص ^3 = ص ^ ( … + … + … ) = ص ^6
4 _ ( 2 3 )^2 × ( 2 3 )^3 = ( 2 3 )^ 5
درس كثيرات الحدود ( متعددة الحدود - الدوريات )
نشاط 1 :
قسم المعلم متعلمي الصف الى مجموعات ثم وزع المعلم على كل مجموعة بعض البطاقات الجبرية و طلب منهم نمذجة ما تعبر عنه البطاقات الجبرية
1 _ مجموعة المتعلم فيصل كان نصيبها من البطاقات هو :

التعبير الجبري للنموذج هو : - س + 2 س + 3
2 _ مجموعة المتعلم بدر كان نصيبها من البطاقات هو :

التعبير الجبري للنموذج هو : 2 س ^2 - 3 س - 4
التعبيرات الجبرية السابق مثل : - س^ 2 + 2 س + 3 نسمي كثير حدود
كثيرة الحدود مقدار جبري هي تعبير جبري يتكون من واحد او اكثر من الحدود الجبرية يتم بناؤها باستخدام عمليات الجمع و الطرح
تدرب 2 :
حدد من التعابير الجبرية التالية ما يمثل حدودية و ما لا يمثل ذلك
1 _ 3 س ^ 5 + 2 س ^ 2 - 6 س …
2 _ 5 س ^ 2 - س ص + ص ^ 2 + 4 ص - 7 …
3 _ ص ^ - 3 س ^2 + س …
4 _ 3 س …
5 _ 3 ^ س + 5 …
تدرب 3 :
اوجد قيمة كل من كثيرات الحدود التالية عندما س = 3 و ص = 2 -
1 _ 1 3 س ^3 + 2 ص^2 + 25 = …..
2 _ 3 ص ^4 - 2 س ص - 50 = ……
اذا كانت س = 7 و ص = 7 و ن = 3 اي المقادير الاتية صحيحة بحيث يكون الناتج 14 ؟
أ _ س × ( ص + ن )
ب _ س × ص × ن
ج _ ن × ص - س
د _ ( ص + ن ) ÷ س
درس جمع كثيرات الحدود و طرحها
نشاط 1 :
سوف نستخدم البطاقات الجبرية لنمذجة كثيرات الحدود بفرض ان :

سنستخدم هذه البطاقات لنمذجة الحدوديات كما في المثال التالي :

2 س ^ 2 + ( - س ) + 3 - س ^ 2 + 3 س + - 2
تدرب 1 :
1 _ اكتب كثيرة الحدود التي تمثل النموذج التالي :

( - 2 س ) + ( - 2 س ) + 4
2 _ نمذج كثيرة الحدود س ^ 3 - 2 س ^ 2 + 4 س - 1 مستخدما البطاقات
س ^ 2 س ^ 2 س ^ 2 س س س س - 1
نشاط 2 :
1 _ سوف نستخدم البطاقات الجبرية لنمذجة كثيرات الحدود بفرض ان :

2 س ^ 2 + ( - س ) + 3 + - س ^ 2 + 3 س + - 2
2 _ بالضم احذف الازواج الصفرية :

3 _ اكتب النمذجة التي حصلت عليها :
وحدة تحليل المقادير الجبرية
درس العامل المشترك الاكبر ( ع م ا )
سوف نتعلم ايجاد العامل المشترك الاكبر ( ع م ا ) لحدين او اكثر كثيرات الحدود
نشاط 1 :
يمكننا ايجاد العامل المشترك الاكبر ( ع م ا ) للعددين 18 و 30 بطريقتين اكمل ما يلي :
الطريقة الاولى : عوامل العدد
عوامل 18 هي : 1 و 2 و 3 و 6 و 9 و 18
عوامل 30 هي : 1 و 2 و3 و 5 و 6 و 10 و 15 و 30
العوامل المشتركة بينهما هي : 1 و 2 و 3 و 6
فإن العامل المشترك الاكبر ( ع م ا ) للعدين 18 و 30 هو 6
الطريقة الثانية : التحليل بالعوامل الاولية
18 = 2 × 3 × 3
30 = 2 × 3 × 5
فإن العامل المشترك الاكبر ( ع م ا ) للعددين 18 و 30 هو 2 × 3 = 6
تذكر ان : الاعداد الاولية : هي الاعداد التي لها عاملان فقط هما الواحد و العدد نفسه العامل المشترك الاكبر ( ع م ا ) لعددين او اكثر هو اكبر عدد يكون عاملا مشتركا لعددين او اكثر
العوامل الاولية للعدد 6 هي : 2 و 3
اوجد العامل المشترك الاكبر ( ع م ا ) للحدين 8 و 12 س
نحلل الحدين الى عواملها الاولية
8 = 2 × 2 × 2
12 س = 2 × 2 × 3 × س = 2^2 × 3 × س
فيكون العامل المشترك الاكبر ( ع م ا ) للحدين 8 و 12 س هو 4
ملاحظة لايجاد العامل المشترك الاكبر ( ع م ا ) لنجموعة حدود الجبرية : نأخذ العامل المشترك الاكبر ( ع م ا ) في جميع الحدود بأصغر أس
درس التحليل باستخراج العامل المشترك الاكبر
سوف تتعلم التحليل باخراج العامل المشترك الاكبر ( ع م ا ) للتعبيرات الجبرية
نشاط 1 :
قال خالد لصديقه جاسم انه يستطيع ايجاد مساحة المستطيلين المرسومين بطريقتين مختلفتين هما :

الطريقة الاولى :

مساحة المستطيلين = 4 × 7 + 4 × 5
= 28 = 20 =48
الطريقة الثانية :
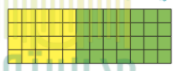
مساحة المستطيلين 4 × 7 + 5 = 4 × 12 = 48
فكر و ناقش :
الشكل المقابل مربع رسمت دائرة نصف قطرها نق تمس اضلاع المربع من الداخل اراد سعود ان يعين مساحة المنطقةالحمراء بدلالة نق ثم ان يقوم بتحليل مقدار الناتج ساعد سعود على حلها

درس تحليل الفرق بين مربعين
نشاط 1 :
ارض مصنع مربعة الشكل مساحتها س^2 وحدة مرعة يراد اخذ غرفة منها مربعة الشكل مساحتها ص^2 وحدة مربعة لاستخدامها كمخزن احسب مساحة المتبقية من ارض المصنع
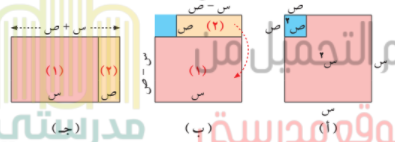
من التمثيل السابق نجد ان :
في الشكل أ : يمثل قطعة الارض التي مساحتها س^2 و موضع الغرفة المراد اخذها و التي مساحتها ص^2
في الشكل ب : يمثل مساحة قطعة الارض المتبقية من المصنع ( س^2 - ص^2 )
و مقسمة الى منطقتين :
1 _ منطقة مستطيلة بعداها س , س - ص وحدة الطول
2 _ منطقة مستطيلة بعداها ص , س - ص وحدة الطول
مساحة قطعة الارض المتبقية = مساحة القطعة 1 + مساحة القطعة 2
= ( س - ص ) ( س + ص ) وحدة مربعة
عموما : الفرق بين مربعي كميتين يساوي حاصل ضرب مجموع الكميتين في الفرق بينهما
درس حل معادلة من الدرجة الاولى في متغير واحد
نشاط 1 :
مما سبق دراسته اكمل حل المعادلات التالية :
1 _ س + 5 = 7
2 _ س - 3 = 14
تدرب 1 :
يعرض احد مواقع الاعلانات فستانا بتصميم معين بمبلغ 12 دينار يضاف اليه 3 دنانير مقابل خدمة التوصيل الى المشتري فاذا ارادت ندى ان تشتري عددا من الفساتين بمبلغ 75 دينارفكم فستانا يمكن ان تشتري ؟
تدريب 2 :
اوجد حل المعادلات التالية :
1 _ 3 س - 4 = - 18 - س
2 _ 5 ( س - 2 ) = 4
وحدة الهندسة و القياس
درس نظرية فيثاغورث و عكسها
نشاط 1 :
في الشكل التالي أ ب ج = 4 وحدة طول من الرسم و باستخدام الوحدات المربعة
اكمل الجدول التالي :
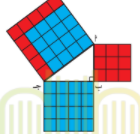
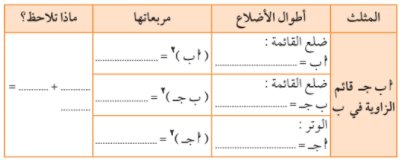
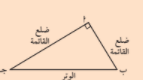
تذكر ان : في المثلثات قائمة الزاوية هما الضلعان اللذان يشلان الزاوية القائمة و الوتر هو اطول ضلع في المثلث و هو الضلع المقابل للزاوية القائمة
نظرية فيثاغورث :
في المثلث القائم الزاوية يكون مربع طول الوتر مساويا لمجموع مربع طولي الضلعين الاخرين
تدرب 1 :
س ص = 6 وحدة طول , س ع = 10 وحدة طول أوجد ص ع
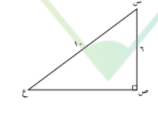
المعطيات :
المطلوب :
البرهان : بما ان س ص ع قائم الزاوية في ص فان :
( س ع ) = ( س ص )^2 + ( ص ع )^2
……… باستخدام العملية العكسية
ص ع = ….. وحدات طول
تدرب 2 :
اذا كان المدينة ب تقه شرق المدينة أ بمسافة 15 كم و كانت المدينة ج تقع في شمال المدينة أ بحيث تبعد عن المدينة ب مسافة 25 كم اوجد المسافة بين المدينتين أ و ج
المعطيات :
المطلوب :
البرهان : ا ب ج مثلث قائم الزاوية في…
المسافة بين المدينتين ا و ج هي…. كم
درس عكس نظرية فيثاغورث :
اذا كان مربع طول الضلع الاطول في مثلث مساويا لمجموع مربعي طولي الضلعين الاخرين فان هذا المثلث قائم الزاوية
اذا كان ( ب ج )^2 = ( ا ج )^2 + ( ا ب )^2 فان المثلث ا ب ج قائم في أ
تدريب :
استخم المصرين القدامى احبالا ذات عقد تكون مثلثا تبلغ اطوال اضلاعه بوحدات الطول 3و 4 و 5 على التوالي لمساعدتهم على تشكيل الزوايا القائمة اثناء بناء الاهرامات وضح كيف يعمل هذا النظام
مربع طول الضلع الاطول ( ب ج )^2 = (…)^2 = 25
مربعا طولي الضلعين الاخرين (… )^2 + (…)^2 = …. +… = ….
النظام يكون زاوية قائم الزاوية
ساعة حائط طول مؤشر الساعات فيها 6 وحدة طول بينما طول مؤشر الدقائق 8 وحدة طول اوجد المسافة بين طرفي المؤشرين عند تمام الساعة الثالثة
عند الساعة الثالثة تكون العقارب قائمة المسافة = …^2 + …^2 =…. + …. = …
المسافة + …. وحدات طول
درس مساحة شبه المنحرف
سوف نتعلم مساحة شبه المنحرف
نشاط 1 :
اراد مزارع ان يضع ملصقا دعائيا على سلة من سعف النخيل اوجهها على شكل شبه المنحرف فاستعان بابنه احمد ليساعده في ذلك و طلب من الاتي :
خذ زوجا متطابقا من شبه المنحرف و دور احدهما 180 درجه حول م و الصق البطاقتين ببعضهما بعضا كما هو موضح في الشكل
سوف نتعلم من نشاط المزارع و ابنه احمد كيفية حساب مساحة شبه المنحرف
1 _ ما اسم الشكل الناتج ؟ …
2 _ ما العلاقة بين مساحة شبه المنحرف و مساحة الشكل الناتج ؟ ….
3 _ ما العلاقة بين ارتفاع و طول قاعدة الشكل الناتج و ارتفاع و طول قاعدة شبه المنحرف ؟ ….
فكر في استنتاج قاعدة لحساب مساحة شبه المنحرف باستخدام الارتفاع و طول القاعدة مما سبق نستنتج :
مساحة شبه المنحرف = مجموع طولي القاعدتين 2 × الارتفاع
معلومة مفيدة : سعف النخيل عبارة عن اوراق شجرة النخيل المركبة و هي ريشية الشكل و طولها يتراوح ما بين 3 لل 6 امتار تقريبا و تنتج النخلة ما بين العشرة و العشرين سعفة في السنة
تدرب 1 :
سم القاعدتين و الارتفاع في كل مما يلي :
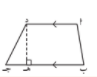 | 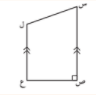 | 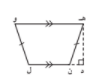 |
| ق1 ب ج | ||
| ق2 أ د | ||
| ع |
حل المسائل : مساحة الاشكال غير المنتظمة
سوف نتعلم ايجاد مساحة الاشكال غير المنتظمة
نشاط 1 :
يمثل الشكل الموضح بالشكل قطعة ارض في احدى ملاعب الجولف الخاصة الصغيرة تريد صاحبة الملعب ان تكسو المنطقة المحددة بعشب جديد

1 _ اوجد الاطوال المجهولة س ص و اشرح كيف اوجدت اطوالها
2 _ ارسم قطعا مستقيمة افقية او رأسية أو مائلة لتقسم الشكل الى اشكال هندسية مألوفة
3 _ اوجد مساحة كل شكل هندسي على حدى ثم اوجد مساحة قطعة الارض الكلية
4 _ قسم قطعة الارض الى اشكال عندسية بطريقة مختلفة ثم اوجد المساحة الكلية هل حصلت على المساحة نفسها ؟
وحدة الاحتمال
درس طرائق العد
سوف تتعلم : مخطط الشجرة البيانية و تنظيم قائمة و مبدأ العد و التبادل و التوافيق
نشاط 1 :
زار خالد المدينة الترفيهية و عند دخوله حصل على هدية عبارة عن تذاكر مجانية للعبتين من اصل اربع لعب متاحة و مختلفة فإذا كانت اللعب الاربع : هي الاعصار و الدردور و البرق و السندباد فبكم طريقة يستطيع خالد اختيار اللعبتين المتاحتين له بشرط عدم تكرار اللعبة ؟
يمكن التوصل الى عدد طرق اختيار خالد للعبتين مناحتين له بعدة طرق منها :
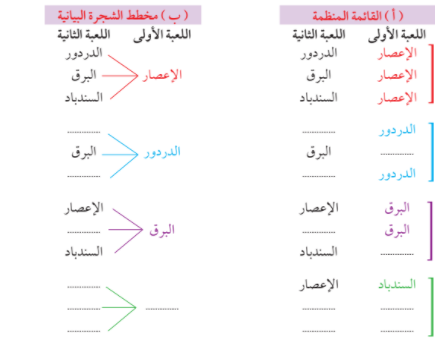
لاحظ أن : عدد طرق اختيار خالدد للعبة الاولى هو 4 طرق و عدد طرق اختيار للعبة الثانية هو 3 طرق و بذلك يستطيع اختيار لعبتين ب 12 طريقة مختلفة
و يمكن ايضا التوصل لعدد طرق اختيار خالد للعبتين متاحتين له بطريقة اخرى و هي :
عدد الطرق = عدد طرق اللعبة الاولى × عدد طرق اختيار اللعبة الثانية
.. × …. = 12 طريقة
هذه الطريقة تسمى مبدأ العد و يفضل العمل بها اذا كان التمثيل بالقائمة المنظمة او بالشجرة البيانية فيه صعوبة لكثرة البيانات المستخدمة و تعددها
مبدأ العد : هو عملية تتكون من خطوتين مستقلتين اذا كان عدد طرق اجراء الخطوة الاول و عدد طرق اجراء الخطوة الثانية فان عدد الطرق الممكنة لاجراء العملي هو :
ن1 × ن2 و يمكن تعميم المبدأ لاكثر من خطوتين
تدرب 1 :
يقدم مطعم وجبات خفيفة من طبق رئيسي اما لحم او سمك او دجاج و كل طبق رئيسي يقدم معه مقبلات من حساء او سلطة
أ _ أكمل مخطط الشجرة البيانية لتبين الوجبات الممكن تقديمها :
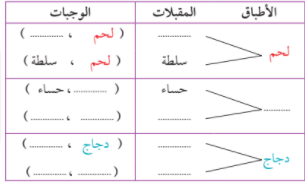
ب _ كم عدد الوجبات التي يمكن تقديمها ؟
عدد الوجبات = … × …. = … وجبات
التباديل و التراتيبات :
نشاط 2 :
اراد خالد التعرف على جميع الاعداد و التي يتكون كل منها من رقمين فقط من مجموعة الارقام 1 و 2 و 3 و 4 على الا يسمح بتكرار الرقم في العدد فهل تستطيع ان تساعده في اكمال مخطط الشجرة التالي ؟

توجد 12 طريقة ممكنة لاختيار الرقمين المسموح بهما لنكون بهما العدد اي ان عدد الطرق = 4 × 3 = 12
لاحظ ان : عند تبديل الرقمين 1 و 2 مثلا حصلنا على العددين 21 و 12 لذلك يكون الترتيب هنا مهم و تسمى كلا منها ترتيبة
مما سبق يكون ترتيب العناصر مهما دون تكرار نسمي هذاالاختيار تبديلا و نرمز له بالرمز ( ل )
من النشاط السابق :
استطعنا مع خالد ان تحصل على 12 طريقة تبديلة لنكون العدد المطلوب عند اختيار عنصران مختلفان من 4 عناصر دون تكرار و مراعاة الترتيب فيهما و يمكننا كتابة ذلك على الصورة الرمزية
أ _ ما هو عدد التبديلات الممكنة لاختيار 3 عناصر من 1 و 2 و 3 و 4 لنكون بها اعدادا من اربعة منازل ؟
عدد التبديلات = 4 × 3 × 2 × 1 = 24 تبديلة
هل لاحظت نمطا معينا في عمليات الضرب السابقة ؟
عملية الضرب على الصورة 4 × 3 × 2 × 1 العوامل تتناقص بمقدار واحد و تنتهي بالعدد واحد و يمكن كتابتها على الصور 4! و تقرأ مضروب 4
مضروب العدد : اختيار ن عصر من بين ن عنصر مختلف و بدون تكرار اي عنصر منها حيث ترتيب مهم سنرمز له بالرمز ن!
التباديل : عند اختيار م عنصر من بين ن عنصر مختلف و من دون تكرار اي عنصر منها حيث ترتيب العناصر مهم .
تدرب 3 :
تستخدم احدى المدن لوحات ترخيص الدرجات و التي تحتوي على عدد مكون من 3 ارقام مختلفة للوحة و باستخدام الارقام من 1 لل 9 يريد المدير المسؤول عن تنظيم الدراجات ان يعرف عدد لوحات التراخيص التي يمكن اصدارها
تمرين : في تدرب 3 اذا سمح المدير المسؤول بتكرار الرقم فكم عد لوحات التراخيص التي يمكن اصدارها ؟
فكر و ناقش :
عرض المعلم المثال التالي : كم عددا مكونا من اربعة ارقام يمكن تكوينه من مجموعة الارقام 0 و 1 و 2 و 3 في حالة السماح بتكرار الارقام وليد يرى ان حل المثال هو :
فأيهما اجابته صحيحة ؟ فسر ذلك ؟
درس فضاء العينة
نشاط 1 :
يمكن لرواد احد المطاعم اختيار وجبة طعام تتكون من طبق رئيسي و مقبلات و حلوى من بين عدة خيارات موضحة في قائمة الطعام المقابلة
أجب عن الاسئلة التالية من خلال قائمة الطعام الموضحة امامك :

1 _ ما عدد خيارات المقبلات ؟
2 _ ما عدد خيارات الطبق الرئيسي ؟
3 _ ما عدد خيارات الحلوى ؟
4 _ ما عدد الوجبات الممكنة التي يقدمها المطعم ؟ … وجبات

