مذكرة إحصاء ثاني عشر أدبي ف2 #أ. محمد الباقوري 2021 2022
مثـال
السؤال : من تجربة إلقاء قطعة نقود ثلاث مرات متتالية وليكن المتغير العشوائي س يعبرعن عدد الصور . أوجد ما يلـي :
( أ ) فضاء العينة .
( ب ) مدى المتغير العشوائي س .
( ج ) نوع المتغير العشوائي س .
الجواب :
مثال
السؤال : في تجربة إلقاء قطعة نقود متماثلة مرتين متتاليتين اذا كان المتغير العشوائي س يعبرعن عدد الصور
فأوجد :
( ا ) فضاء العينة .
( ب ) مدى المتغير العشوائي س .
( ج ) احتمال وقوع كل عنصر من عناصر فضاء العينة ف .
( د ) دالة التوزيع الاحتمالي للمتغير العشوائي س
الجواب :
مثال
السؤال : إذا كانت دالة التوزيع الاحتمالي د للمتغير العشوائي س هي
| س | 10 | 0 | 1 | 2 | 3 |
| د ( س ) | 0.01 | 0.03 | ك | 0.2 | 0.3 |
أوجد قيمة ك ؟
الجواب :
مثال
السؤال :إذا كان س متغيرا عشوائيا متقطعا مداه هو : ( 1 , 2 , 3 , 4 ) وكان د ( 1 ) = 1 ,0 , د( 3 ) = 4 ,0 , د( 4 ) = 2 , 0 فأوجد د ( 2 )ثم اكتب دالة التوزيع الاحتمالي د للمتغير العشوائي س .
الجواب :
مثـال
السؤال : صندوق يحتوي علي 10 كرات متماثلة منها 7 كرات بيضاء و3 كرات حمراء . سحبت عشوائيا 3 كرات معامن الصندوق . إذا كان المتغير العشوائي س يمثل عدد الكرات البيضاء , فأوجد ما يلي :
( أ ) عدد عناصر فضاء العينة ( ف )
( ب ) مدي المتغير العشوائي س .
( ج ) احتمال كل عنصر من عناصر مدى المتغير العشوائي س .
( د ) دالة التوزيع الاحتمالي د للمتغير العشوائي س .
الجواب :
السؤال : إذا كانت دالة التوزيع الاحتمالي د للمتغير العشوائي المتقطع س هي :
فأوجد التوقع μ للمتغير العشوائي س .
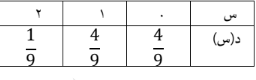
الجواب :
السؤال : إذا كان فضاء العينة لأربع أسر لديها طفالن كالتالي:
ف = ( ولد ، ولد) ، ( ولد،بنت ) ، ( بنت،ولد) ،( بنت،بنت ) فأوجد :
( أ ) مدى المتغير العشوائي المتقطع س الذي يعبر عن عدد الاولاد.
( ب ) احتمال كل عنصر من عناصر مدى المتغير العشوائي س .
( ج ) دالة التوزيع الاحتمالي د للمتغير العشوائي المتقطع س .
( د ) التوقع μ للمتغير العشوائي س
الجدول التالي يبين دالة التوزيع الاحتمالي لمتغير عشوائي متقطع س
| س | 2 | 3 | 4 | 5 |
| د ( س ) | 0.1 | 0.3 | 0.5 | 0.1 |
أوجد :
( أ ) التوقع( μ )
( ب ) التباين ( 2σ )
( ج ) الانحراف المعياري ( σ )
الجواب :
السؤال : الجدول التالي يبين دالة التوزيع الاحتمالي للمتغير عشوائي متقطع س .
| س | 1 | 2 | 3 | 4 | 5 |
| د ( س ) | 0.2 | 0.1 | 0.3 | 0.1 | 0.3 |
أوجد : ( أ ) التوقع( μ )
( ب ) التباين ( 2σ )
( ج ) الانحراف المعياري ( σ )
الجواب :
السؤال : الجدول التالي يبين دالة التوزيع الاحتمالي للمتغير عشوائي متقطع س .
| س | 1 | 2 | 3 | 4 | 5 |
| د ( س ) | 0.43 | 0.29 | 0.17 | 0.09 | 0.02 |
أوجد : ت ( 1 ) ، ت ( 3.5 ) ، ت ( 4 ) ، ( 5 )
الجواب :
السؤال : الجدول التالي يبين دالة التوزيع الاحتمالي للمتغير عشوائي متقطع س .
| س | -1 | 3 | 5 | 7 |
| د ( س ) | 0.1 | 0.45 | 0.7 | 1 |
أوجد :
( أ ) ل ( -1 < س > 5 )
( ب ) ل ( 3 ≤ س > 7 )
( ت ) ل ( س < 3 )
الجواب :
السؤال : لتكن د هي دالة التوزيع الاحتمالي للمتغير العشوائي س كما في الجدول التالي :
| س | 1 | 2 | 3 | 4 |
| د ( س ) | 0.4 | 0.2 | 0.1 | 0.3 |
ارسم بيان دالة التوزيع الاحتمالي للمتغير العشوائي س
الجواب :

السؤال : لتكن د هي دالة التوزيع الاحتمالي للمتغير العشوائي س كما في الجدول التالي :
| س | 1 | 2 | 3 | 4 | 5 |
| د ( س ) | 0.5 | 0.1 | 0.2 | 0.15 | 0.05 |
( أ ) أوجد دالة التوزيع التراكمي ت .
( ب ) ارسم بيان دالةالتوزيع التراكمي ت .
الجواب :
السؤال : إذا كان س متغيرا عشوائيا ذو حدين معلمتيه هما ن = 8 ، ل = 2 ، 0 فأوجد : ( أ ) ل( س = 2 ) ، ( ب) ل ( 2 ≤س > 4)
الجواب :
السؤال : إذا كان س متغيرا عشوائيا ذو حدين معلمتيه هما ن = 10 ، ل = 5 ، 0 فأوجد :( أ ) ل ( س = صفر ) ، ( ب ) ل( 2<س ≥4 )
الجواب :
السؤال : في تجربة القاء قطعة نقود 10 مرات متتالية , احسب احتمال ظهور كتابة 4 مرات
الجواب :
السؤال : عند إلقاء حجر نرد منتظم 7 مرات متتالية ، أوجد :
( أ ) احتمال ظهور العدد 2 خمس مرات .
( ب ) احتمال ظهور العدد 2 مرة واحدة على الاقل .
( < ) احتمال ظهور العدد 2 مرة واحدة على الاكثر .
الجواب :
قوانين توزيع ذات الحدين

مثال
السؤال : ينتج مصنع سيارات 350 سيارة يوميا , إذا كانت نسبة السيارات المعيبة 02 ,0 فأوجد التوقع والتباين و الانحراف المعياري لعدد السيارات المعيبه في يوم واحد .
الجواب :
مثال
السؤال : في تجربة إلقاء قطعة نقود متماثلة 8 مرات . أوجد التوقع والتباين والانحراف المعياري إذا كان المتغير العشوائي س هو ظهور صورة .
الجواب :
مثال
السؤال : إذا رمينا قطعة نقود معدنية متماثلة 12 مرة .
( أ ) احسب احتمال الحصول على صورة 7مرات .
( ب ) أوجد التوقع و التبايــــــن .
الجواب :
مثال :
السؤال : 70 % من زبائن مطعم ما أفادو بأن الطعام قد أعجبهم وسيقصدونه مرة أخرى من بين 100 زبون , أوجد التوقع و التباين والانحراف المعياري
الجواب :
السؤال : في أحد مصانع الا طارات تبين أن 5 % من ألاطارات غير صالحة للاستعمال . إذا سحبنا 10 إطارات , فأوجد التوقع والتباين للاطارات غير الصالحه
الجواب :
المتغيرات العشوائية تنقسم إلى

حدد ما إذا كانت المتغيرات العشوائية التالية متصلة أو متقطعة :
( أ ) الزمن( بالثواني ) الذي يتطلبه حاسوب ليفتح ملف ما .
( ب ) المعدل السنوي للأمطار في بلد معين .
( ج ) الزمن المستغرق لرحلة طائرة من بلد معين إلى بلد آخر.
( د ) سعر صفيحة الوقود .
( هـ ) عدد الاحرف في أي كلمة .
إذا كان س متغيرا عشوائيا متصلا و دالة كثافة الاحتمال له هي :

فأوجد :
( أ ) ل ( 2 ≤ س ≥ 4 )
( ب ) ل ( س ≤ 5 , 2 )
الجواب :
السؤال : إذا كان س متغيرا عشوائيا متصلا ودالة كثافة الاحتمال له هي :
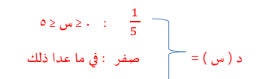
فأوجد :
( أ ) ل ( 0 ≤ س ≥ 5 )
( ب ) ل ( س = 3 )
( ج ) ل ( س ≥ 2 )
( د ) ل ( س < 2 )
الجواب :
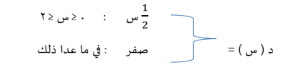
السؤال : إذا كان س متغيرا عشوائيا متصلا ودالة كثافة الاحتمال له هي :
أوجد :
( أ ) ل ( س > 1 )
( ب ) ل ( س ≤ 1 )
( ج ) ل ( س = 1 )
الجواب :
السؤال : لتكن الدالة د :

( أ ) أثبت أن الدالة د هي دالة كثافة احتمال .
( ب ) أثبت أن الدالة د تتبع التوزيع الاحتمالي المنتظم .
( ج ) أوجد ل ( 0 < س ≥ 3 )
( د ) أوجد التوقع والتباين للدالة د .
الجواب :
السؤال : الدالة د تتبع التوزيع الاحتمالي المنتظم :

( أ ) أثبت أن هذه الدالة هي دالة كثافة .
( ب ) أوجد ل ( 1 ≤ س ≥ 2 . )
( ج ) أوجد التوقع والتبايــن .
الجواب :
السؤال : إذا كان ق يتبع التوزيع الطبيعي المعياري للمتغير العشوائي س فأوجد :
( أ ) ل ( ق ≥16 ,2 )
( ب ) ل ( ق ≤ 51 ,2 )
( ج ) ل ( 5 ,1 ≤ ق ≥ 4 , 2 )
( د ) ل ( ق ≥ 95 ,0)
( هـ ) ل ( ق < 71 ,0 )
( و ) ل ( 45 ,1 ≤ ق ≥ 26 ,3 )
الجواب :
السؤال : إذا كان ق يتبع التوزيع الطبيعي المعياري للمتغير العشوائي س فأوجد :
( أ ) ل ( ق ≤ 2.16 )
( ب ) ل ( -7.1 ≤ ق ≤ 2.58 )
( ج ) ل ( -23 .1 ≤ ق ≤ 0.68 )
الجواب :
السؤال : يمثل المتغير العشوائي س درجات الطالب في إحدي المواد الدراسية , إذا كان توزيع درجاته يتبع التوزيع الطبيعي الذي وسطه μ = 50 وانحرافه المعياري σ = 10 فأوجد :
( أ ) ل ( 40 < س > 76 )
( ب ) ل ( س ≥ 55 )
الجواب :
السؤال : متغير عشوائي متصل س يتبع توزيعا طبيعيا , التوقع μ = 37 , وتباينه O2 = 16 , أوجد :
( أ ) ل ( 30 < س > 35 )
( ب ) ل ( 35 < س > 40)
( ج ) ل ( س < 30 )
الجواب :
السؤال : يمثل المتغير س الزمن الذي يستغرقه أحد الطلاب للوصول إلى المدرسة وهو متغير عشوائي يتبع التوزيع الطبيعي توقعه μ = 15 والتباين o 2 = 9 . احسب احتمال وصوله ب :
( أ ) أقل من 18 دقيقه .
( ب ) أكثر من 18 دقيقة .
( ج ) أكثر من 12 دقيقة وأقل من15 دقيقه
الجواب :
المتباينات و البرمجة الخطية
السؤال : أوجد مجموعة حل المتباينات التالية ومثل مجموعة الحل علي خط الاعداد الحقيقية .
( أ ) 3+ س ≥ 7
( ب ) -11 < 3س - 2≤ 4
( < ) 13- 5 س < 8
الجواب :
السؤال : بين أيا من النقاط التالية : أ ( 2 , 1 ) , ب ( 7 , 0 ) , ) جـ ( -1 , 2 . ) تحقق المتباينة
3س + 5 ص ≤ 12
الجواب :
السؤال : ارسم خط الحدود لكل متباينة
أ- ص + س < 5
الجواب :

ب- 3س + 2ص ≥ 18
الجواب :

ج- ص ≤ 3 – 2س
الجواب :

د- س – ص – 2 < 0
الجواب :

السؤال : مثل بيانيا منطقه الحل لكل متبانية
أ- س + ص < 3

ب- س – 3ص ≥ 6

السؤال : مثل بيانيا منطقه الحل المشترك للمتباينتين :
س + ص > 3

5س + 2ص ≤ 10


السؤال : مثل بيانيا منطقة الحل المشترك للمتباينات التالية :
س + ص ≥ 2 ، س –ص ≤ 3 ، ص ≤ 0


تدريب
السؤال : مثـــل بيانيا منطقة الحل المشترك للمتباينتين
( أ ) س + 2ص ≤ 4 ، ص ≥ -س -1
( ب ) ص < س + 2 ، ص ≥ -س + 1
( جـ ) ص ≥س + 3 ، ص ≤س + 2
( د ) س – 2ص > 3 ، 2س + ص < 8
( هـ ) ص > س – 3 ، ص ≤س – 4
( و ) – 2س + ص < 1 ، ص < س
الجواب :
السؤال : مثل بيانيا" منطقة الحل المشترك للمتباينات التالية :
( أ ) س + ص ≥ 2 ، س –ص < 1 ، 2س + 3ص > 6
( ب ) س ≤ ص ، 2س + ص ≥ 2 ، ص + 1 < 3
( جـ ) س + ص ≤ 3 ، س –ص ≥ 4 ، ص ≥ 0
الجواب :
البرمجة الخطية
السؤال : أوجد بيانيا مجموعة حل المتباينات التالية :
س ≥ 0 ، ص ≥ 0 ، س+2ص≤ 6 ، 3س+2ص≤ 12
ثم أوجد من مجموعة الحل قيم( س ، ص ) التي تجعل دالة الهدف هـ أكبر ما يمكن حيث هـ = 6س + 4ص
الجواب :


السؤال : أوجد بيانيا مجموعة حل المتباينات التالية :
س ≤ 0 ، ص ≤ 0 ، س + ص ≥ 5 ، س + 2ص ≥ 8
ثم أوجد من مجموعة الحل قيم ( س ، ص ) التي تجعل دالة الهدف هـ أصغر ما يمكن ، حيث هـ = س + 3ص
الجواب :
تمارين متنوعة
السؤال : أوجد بيانيا مجموعة حل المتباينات التالية
س ≥ 0 ، ص ≥ 0 ، 3 س + 2 ص ≤ 6 ، 2س +3 ص ≤ 6
ثم أوجد من مجموعة الحل قيم ( س ، ص ) التي تجعل دالة الهدف هـ أصغر ما يمكن ، حيث هـ = 3س + 4ص
الجواب :
السؤال : أوجد بيانيا مجموعة حل المتباينات التالية
س ≥ 0 ، ص ≥ 0 ، 4 س + 2 ص ≤ 4 ، 2س +4 ص ≤ 4
ثم أوجد من مجموعة الحل قيم ( س ، ص ) التي تجعل دالة الهدف هـ أكبر ما يمكن ، حيث هـ = 3س + ص
الجواب :
السؤال : أوجد بيانيا مجموعة حل المتباينات التالية
س ≥ 0 ، ص ≥ 0 ، س + ص ≤ 5 ، 4س +ص ≤ 8
ثم أوجد من مجموعة الحل قيم ( س ، ص ) التي تجعل دالة الهدف هـ أصغر ما يمكن ، حيث هـ = س + 3ص
الجواب :
السؤال :في الشكل المقابل : أوجد قيم ( س , ص ) التي تجعل دالة الهدف هـ قيمة عظمى أوقيمة صغرى حيث : داله الهدف هـ = 6س + 2ص
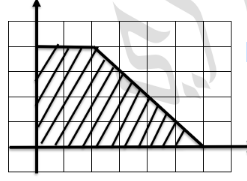
الجواب :

