1
في الشكل السابق مثلث (أ ب جـ) فيه (م) نقطة تقاطع المحاور ، ب جـ = 15 سم، (جـ م ب) ̂ = 60
فان م أ =
2
نقطة تقاطع محاور أضلاع المثلث القائم الزاوية تقع منتصف الوتر
3
هرم منتظم قاعدته مربعة الشكل طول ضلعها 6 سم وارتفاع الهرم 10 سم
فان مساحة القاعدة =
4
هرم منتظم قاعدته مربعة الشكل طول ضلعها 5 سم وارتفاع الهرم 6 سم فان حجم الهرم =
8
أوجد القيمة الأصلية لسلعة تبلغ قيمتها النهائية 300 دينار بعد أن تناقص سعرها بنسبة 40%
9
• إذا كانت القيمة الأصلية لسهم أحد الشركات 400 فلس والنسبة المئوية لتزايد قيمة السهم 14% فإن القيمة النهائية للسهم
13
نقطة تقاطع الأعمدة المرسومة من رؤوس المثلث القائم الزاوية هي رأس الزاوية القائمة
14
بلغ سعر التذكرة الواحدة لحضور مسرحية 50 دينار ويضاف إليها نظير الخدمة.
فان سعر التذكرة عند خصم 20% ثم إضافة 12% نظير خدمة =
15
إذا انخفض سعر سلعة نفسه 5% ثم ارتفع بنسبة 5% فإن سعر السلعة سيعود إلى سعرها الأصلي
20
أوجد ميل المستقيم المار بالنقطتتين (-2، 1) (-3، -4)
21
الجزء المقطوع من محور الصادات للمستقيم الذي معادلته 3 ص = 6 س +9
22
إذا كانت معادلة المستقيم ك هي ص = 2 س -1
ومستقيم ل مار بالنقطتتين (1، 2) (3، 1)
هل المستقيمان متوازيان؟
23
اذا كان ميل المستقيم ل = 5/-2 فان ميل المستقيم العمودى عليه =
24
كرة حجمها 288 π سم3 فإن نصف قطرها
25
كرة نصف قطرها 5 سم، فان حجم الكرة
28
في الشكل المجاور مثلث (أ ب جـ) فيه أ ب = أ جـ = 10 سم، (د) منتصف (أ ب)، دهـ = 4 سم ، ( ب) ̂= 45
فان أ هـ = 4 سم ؟
30
بيان الدالة ص = - س2 -1 هو انعكاس للدالة ص = س2 في محور السينات ثم إزاحة رأسية وحدة نحو الأعلى
31
التمثيل البيانى للدالة التربيعة ص = (س+1)2 هو :
32
إذا كان السعر الأصلي لدراجة 36 دينار وكان عليها خصم 10% فإن سعر البيع 36 دينار
34
يقيم متجر عرض خاص على الأدوات الكهربائية، إذ يخصم 19 % من سعرها الأصلي، فان قيمة خصم الراديو علماً أن سعرها الأصلي 49.5 دينار ≈
35
إذا كانت المجموعة الشاملة ش = {5، 10، 15، 20، 25، 30}
ع = {5، 15، 30}
فان ش ∩ ع =
36
اذا كانت : ش = {2، 4، 6، 8، 10، 12}
س = {8، 6، 4، 2}
فان ش ∩ س = {10، 12}
37
إذا كان س = { أ: أ ∋ ص، 9> أ > 4} حيث أن ص مجموعة الأعداد الصحيحة ، ع = {1، 3، 6، 9، 10}
فان س =
38
فى الشكل المجاور
س ∪ ص = 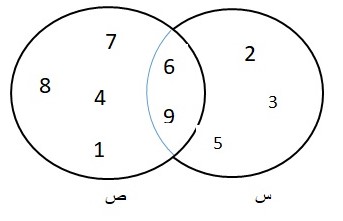
39
إذا كانت س = {1، 3، 4}
ص = {3، 9، 16}
التطبيق ت: س ص : حيث ت(س) = 3 س
فان التطبيق ت كمجموعة من الأزواج المرتبة =
40
إذا كانت س = {1، 3، 4}
ص = {3، 9، 16}
التطبيق ت: س ص : حيث ت(س) = 3 س
فان تمثيل التطبيق ت بمخطط سهمي